13.01. General Linear Lists
General linear list : a list in which operations, such as retrievals, insertions, changes, and deletions, can be done anywhere in the list
Basic operations : Insertion, deletion, retrieval, traversal, ETC
13.01.1. Insertion
- In ordered list : maintained in sequence according to data : Key: one or more field that identifies the data (ex: SSN)
- In random list : No sequential relationship between elements
13.01.2. Deletion
Deletion requires search to locate the data to delete
13.01.3. Retrieval
- Retrieval : provides a data without changing list
- Search : finding an element in a list by some key
13.01.4. Traversal
- Traversal : process of visiting each element in a list in sequence to do something
- Ex) print all elements in a list : Requires looping algorithm
13.02. List ADT
Objects
- A finite ordered list with zero or more elements
Operation
- List CreateList() : Create an empty List
- void AddNode(List list, Element data) : Add a new data element
- void RemoveNode(List list, Element data) : Remove an element
- Element SearchList(List list, Element key) : Find a data element
- void DestroyList(List list) : Destroy a List
- bool TraverseList(List list, int fromWhere, Element data) : Provide next data to traverse list; Return false if end of list Otherwise, yes
- int ListCount(List list) : Return # of elements
- bool IsEmptyList(List list) : If list is empty, return true otherwise, return false
- bool IsFullList(List list) : If list is full, return true otherwise, return false
13.03. Implementation of List
Array implementation of list
- Simple
- Easy to access elements
- Insertion and deletion are inefficient
Linked list implementation of list
- Easy to insert/delete data at any location
13.03.1. Data node
Data (including key) + pointer to next node
typedef struct tListNode {
Element key;
// Data fields, such as …
// char studentNumber[10];
// char studentName[10];
// …
struct tListNode *link;
} ListNode;
13.03.2. Head node
Head pointer + meta data (# of elements)
typedef struct {
int count;
ListNode *head;
} List;
13.03.3. Operations
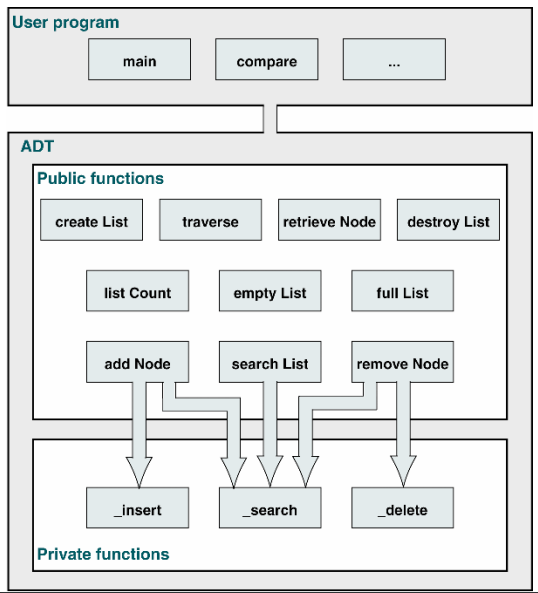
13.03.4. Model for an Abstract Data Type
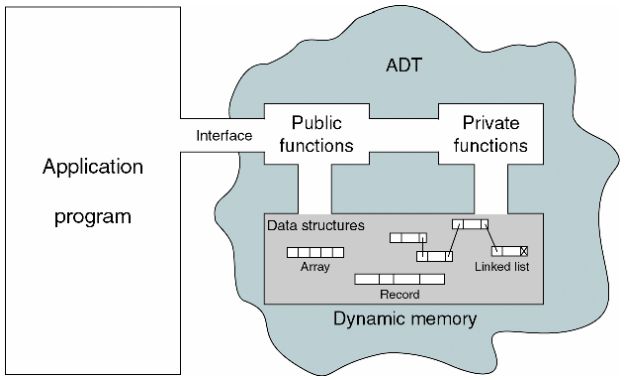
13.03.5. Operations : CreateList
List *createList()
{
List *pNewList = (List*)malloc(sizeof(List));
if(pNewList == NULL)
return NULL;
pNewList->count = 0;
pNewList->head = NULL;
return pNewList;
}
13.03.6. Operations : Insertion
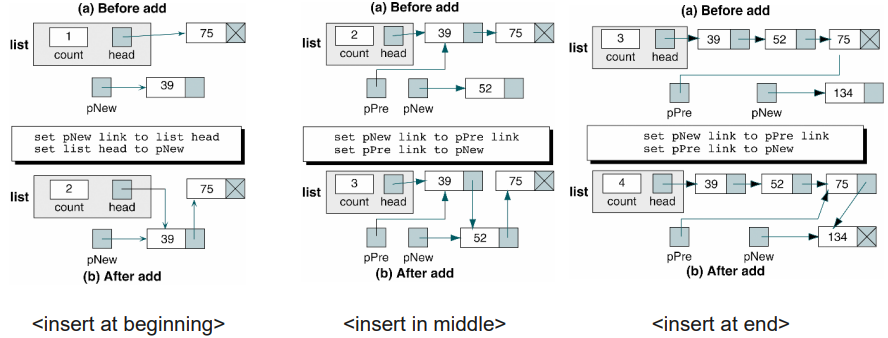
void _insertList(List *pList, ListNode *pPre, Element data)
{
ListNode *pNewNode = (ListNode*)malloc(sizeof(ListNode));
pNewNode->data = data;
if(pPre == NULL){ // insert before head node
pNewNode->next = pList->head;
pList->head = pNewNode;
} else {
pNewNode->next = pPre->next;
pPre->next = pNewNode;
}
pList->count++;
}Insert into Empty List
- When the head pointer of the list is null, the list is empty.
- To add a new node, the list header pointer should be assigned the address of the allocated node and make sure that its link field is a null pointer.
Insert at Beginning
- A new node is added before the first node of the list.
- Determine that addition is at the beginning of the list by testing the predecessor pointer : If the predecessor pointer is a null pointer, there is no predecessor, so we are at the beginning of the list.
- Point the new node to the first node of the list and then set the head pointer to point to the new first node.
- Logically inserting into an empty list is same as inserting a the beginning.
Insert in Middle
- When we add a node anywhere in the middle of the list, the predecessor pointer contains an address
- Point the new node to its successor and then point its predecessor to the new node. The address of the new node’s successor can be found in the predecessor’s link field.
Insert at End
- When adding at the end of the list, we only need to point the predecessor to the new node. There is no successor
- The new node’s link field should be set to null pointer. Also, the last node in the list has a null pointer. If we use this pointer rather than a null pointer constant, the code becomes same as the inserting in the middle.
13.03.7. Operations : Search
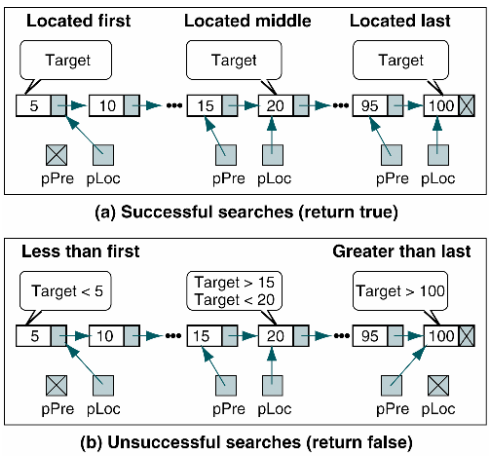
//Incorrect solution
bool _searchList(List *pList, ListNode *pPre, ListNode *pLoc, Element data)
{
// if(pList->count == 0) : should be erased
// return FALSE;
for(pPre = NULL, pLoc = pList->head; pLoc != NULL; pPre = pLoc, pLoc = pLoc->next){
if(pLoc->data == data) // data was found
return TRUE;
else if(pLoc->data > data)
break;
}
return FALSE;
}
void addNodeList(List *pList, Element data)
{
ListNode *pPre = NULL, *pLoc = NULL;
bool found = _searchList(pList, pPre, pLoc, data);
if(!found)
_insertList(pList, pPre, data);
}
void addNodeList(List *pList, Element data)
{
ListNode *pPre = NULL, *pLoc = NULL;
bool found = _searchList(pList, &pPre, &pLoc, data);
if(!found)
_insertList(pList, pPre, data);
}
bool _searchList(List *pList, ListNode **ppPre, ListNode **ppLoc, Element data)
{
for(*ppPre = NULL, *ppLoc = pList->head; *ppLoc != NULL; *ppPre = *ppLoc, *ppLoc = (*ppLoc)->next){
if((*ppLoc)->data == data) // data was found
return TRUE;
else if((*ppLoc)->data > data)
break;
}
return FALSE;
}A list search
- is used to locate data in a list
- To insert data, we need to know the logical predecessor to the new data.
- To delete data, we need to find the node to be deleted and identify its logical predecessor.
- To retrieve data from a list, we need to search the list and find the data.
We must use a sequential search because there is no physical relationship among the nodes.
- The classic sequential search returns the location of an element when it is found and the address of the last element when it is not found.
- Because the list is ordered, we need to return the location of the element when it is found and the location where it should be placed when it is not found.
13.03.8. Operations : Deletion
Delete a data from an ordered list
- Find the location of the node : Directly preceding node is necessary
- Delete node after the preceding node

void _deleteList(List *pList, ListNode *pPre, ListNode *pLoc)
{
if(pPre == NULL)
pList->head = pLoc->next;
else
pPre->next = pLoc->next;
free(pLoc);
pList->count--;
}
void removeList(List *pList, Element data)
{
ListNode *pPre = NULL, *pLoc = NULL;
bool found = _searchList(pList, &pPre, &pLoc, data);
if(found)
_deleteList(pList, pPre, pLoc);
}Delete Node algorithm
- Logically removes a node from the list by changing pointers and then physically deleting the node from dynamic memory.
- Locate the node to be deleted by knowing its address and its predecessor’s address.
- Change the predecessor’s link field to point to the deleted node’s successor
- We then recycle the node back to dynamic memory.
If deleting the only node in the list, results in empty list and set the head to a null pointer
The delete situations
- The only node, the first node, a node in the middle, or the last node of the list
Delete First Node
- When deleting first node, the head pointer must be reset to point to the node’s successor and then recycle the memory for the deleted node
General Delete Case
- Deleting in the middle or at the end is a general case
- Simply point the predecessor node to the successor of the node being deleted.
- When the node being deleted is the last node of the list, its null pointer is moved to the predecessor’s link field, making the predecessor the new logical end of the list
13.03.9. Operations : Traverse
Starting from first node, examine each node in succession until the last node has been processed
bool traverseList(List *pList, int fromWhere, Element *pDataOut);
pList: an ordered list
fromWhere: if fromWhere == 0, return first data
pDataOut: an address to receive the next data
Return value: TRUE if next node exists, otherwise, FALSE
bool traverseList(List *pList, int fromWhere, Element *pDataOut)
{
if(fromWhere == 0 || pList->pos == NULL)
pList->pos = pList->head;
else
pList->pos = pList->pos->next;
if(pList->pos != NULL){
*pDataOut = pList->pos->data;
return TRUE;
}
else {
*pDataOut = 0;
return FALSE;
}
}Traversal
- starts at the first node and examines each node in the succession until the last node has been processed
- Any application that requires that the entire list be processed uses a traversal : Ex) changing a value in each node, printing the list, summing a field in the list, calculating the average, etc.
- We need a walking pointer (a pointer that moves from node to node as each element is processed)
13.03.10. Operations : Destroy
void destroyList(List *pList)
{
ListNode *pDel = NULL, *pNext = NULL;
for(pDel = pList->head; pDel != NULL; pDel = pNext){
pNext = pDel->next;
free(pDel);
}
free(pList);
}
When the list is no longer needed and the application is not done, the list should be destroyed.
Destroy list
- deletes any nodes still in the list and recycles their memory and set the metadata to a null list condition
13.04. Generic Coding
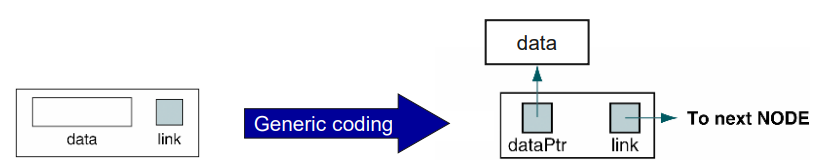
typedef struct node {
void* dataPtr;
struct node* link;
} NODE;
typedef struct {
int count;
NODE* head; // list head
NODE* pos; // for traverse
NODE* rear; // for convenient
int (*compare) (void* argu1, void* argu2);
} LIST;
13.04.1. Type-dependent operation
int (*compare) (void* argu1, void* argu2);
int compareInt(void *argu1, void *argu2)
{
return *(int*)argu1 - *(int*)argu2;
}
int compareStr(void *argu1, void *argu2)
{
return strcmp((char*)argu1, (char*)argu2);
}
bool _searchList(List *pList, ListNode **ppPre, ListNode **ppLoc, Element data)
{
for(*ppPre = NULL, *ppLoc = pList->head; *ppLoc != NULL; *ppPre = *ppLoc, *ppLoc = (*ppLoc)->next){
if((*compare)((*ppLoc)->data, data) == 0) // data was found
return TRUE;
else if((*compare)((*ppLoc)->data, data) > 0)
break;
}
return FALSE;
}
13.04.2. Operations : Create
LIST* createList (int (*compare) (void* argu1, void* argu2))
{
LIST* list = NULL;
list = (LIST*) malloc (sizeof (LIST));
if (list){
list->head = NULL;
list->pos = NULL;
list->rear = NULL;
list->count = 0;
list->compare = compare;
} // if
return list;
} // createList
13.04.3. Operations : Search
bool _search (LIST* pList, NODE** pPre, NODE** pLoc, void* pArgu)
{
// Macro Definitions
#define COMPARE \
( ((* pList->compare) (pArgu, (*pLoc)->dataPtr)) )
#define COMPARE_LAST \
((* pList->compare) (pArgu, pList->rear->dataPtr))
int result;
*pPre = NULL;
*pLoc = pList->head;
if (pList->count == 0)
return false;
// Test for argument > last node in list
if ( COMPARE_LAST > 0)
{
*pPre = pList->rear;
*pLoc = NULL;
return false;
} // if
while ( (result = COMPARE) > 0 )
{
// Have not found search argument location
*pPre = *pLoc;
*pLoc = (*pLoc)->link;
} // while
if (result == 0)
// argument found--success
return true;
else
return false;
} // _search
13.04.4. Operations : Insert
bool _insert (LIST* pList, NODE* pPre, void* dataInPtr)
{
NODE* pNew = NULL;
// allocate a node for data
if (!(pNew = (NODE*)malloc(sizeof(NODE))))
return false;
pNew->dataPtr = dataInPtr;
pNew->link = NULL;
if (pPre == NULL){
// Adding before first node or to empty list.
pNew->link = pList->head;
pList->head = pNew;
if (pList->count == 0)
// Adding to empty list. Set rear
pList->rear = pNew;
} // if pPre
else {
// Adding in middle or at end
pNew->link = pPre->link;
pPre->link = pNew;
// Now check for add at end of list
if (pNew->link == NULL)
pList->rear = pNew;
} // if else
(pList->count)++;
return true;
} // _insert
13.04.5. Operations : Delete
void _delete (LIST* pList, NODE* pPre, NODE* pLoc, void** dataOutPtr)
{
*dataOutPtr = pLoc->dataPtr; // provides deleted data
if (pPre == NULL)
// Deleting first node
pList->head = pLoc->link;
else
// Deleting any other node
pPre->link = pLoc->link;
// Test for deleting last node
if (pLoc->link == NULL)
pList->rear = pPre;
(pList->count)--;
free (pLoc);
return;
} // _delete
13.05. Complex Implementations
13.05.1. Circularly linked lists
- The last node’s link points to the first node of the list
- are primarily used in lists that allow access to nodes in the middle of the list without starting at the beginning
Insertion and deletion from a circularly linked list
- Follow the same logic patterns used in a singly linked list
- except that the last node points to the first node.
- Therefore, when inserting or deleting the last node, we must point the link field to the first node
If the search target lies before the current node?
- In the singly linked list, when we arrive at the end of the list the search is complete
- In the circularly linked list, automatically continue the search from the beginning of the list
13.05.2. Doubly linked lists
- is a linked list structure in which each node has a pointer to both its successor (forward pointer) and its predecessor (backward pointer)
Insertion
- Follows the basic pattern of inserting a node into a singly linked list, but we also need to connect both the forward and the backward pointers
To insert a node into a null list
- The head and rear pointers to point to the new node
To insert a node between two nodes
- The head structure is unchanged
- The new node needs to be set to point to both its predecessor and its successor,
- and they need to be set to point to the new node
To insert a node at the end of the list
- The forward pointer of the new node is set to null
- The rear pointer in the head structure must be set to point to the new rear node
13.05.3. Multilinked lists
- Is a list with two or more logical key sequences
- The same set of data can be processed in multiple sequences
'학부공부 > Algorithm_알고리즘' 카테고리의 다른 글
| 12. Linked List(1) (2) | 2022.02.06 |
|---|---|
| 11. Binary Search & Parametric Search(1) (6) | 2022.01.12 |
| 10. Dynamic Programming(2) (3) | 2021.12.17 |
| 09. Dynamic Programming(1) (6) | 2021.12.15 |
| 08. Divide and Conquer(2) (14) | 2021.11.21 |



댓글