Brute Force and Exhaustive Search
01. Brute Force
A straightforward approach to solving a problem, usually directly based on the problem’s statement and definitions of the concepts involved
- “just do it!”
- the brute-force strategy is the one that is easiest to apply
Examples:
- Computing 𝒂^𝒏(𝒂>𝟎, 𝒏 a nonnegative integer) : multiplying 1 by 𝑎 𝑛 times
- Computing 𝒏!
- The consecutive integer checking algorithm for gcd(𝑚, 𝑛)
- Matrix multiplication
- Searching for a key of a given value in a list
Though rarely a source of clever or efficient algorithms, the brute-force approach should not be overlooked as an important algorithm design strategy
- brute force is applicable to a very wide variety of problems
- for some important problems, it yields reasonable algorithms of at least some practical value with no limitation on instance size (e.g., sorting, searching, matrix multiplication, string matching)
- the expense of designing a more efficient algorithm may be unjustifiable if only a few instances of a
- problem need to be solved and it can solve those instances with acceptable speed
- even if too inefficient in general, it can still be useful for solving small-size instances of a problem
- It can serve an important theoretical or educational purpose as a yardstick with which to judge more efficient alternatives
02. Sorting
A sorting problem
- given a list of n orderable items (e.g., numbers, characters from some alphabet, character strings), rearrange them in nondecreasing order
“What would be the most straightforward method for solving the sorting problem?”
- Selection sort and bubble sort seem to be the two prime candidates
- (Reasonable people may disagree on the answer to this question)
Selection Sort
- Scan the array to find its smallest element and swap it with the first element
- Then, starting with the second element, scan the elements to the right of it to find the smallest among them and swap it with the second elements
- Generally, on pass 𝑖 (0≤ 𝑖 ≤ 𝑛−2), find the smallest element in 𝐴[𝑖..𝑛−1] and swap it with 𝐴[𝑖]:
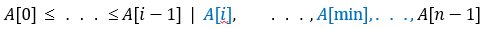
- After 𝑛−1 passes, the list is sorted

- Input size: the number of elements 𝑛
- Basic operation: the key comparison
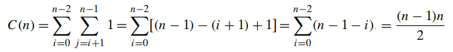
- Selection sort is a O(n^2) algorithm on all inputs.
- However, the number of key swaps is only 𝑛−1. This property distinguishes selection sort positively from many other sorting algorithms.
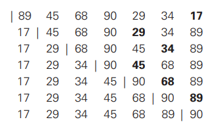
Bubble Sort
- Compare adjacent elements of the list and exchange them if they are out of order
- By doing it repeatedly, we end up “bubbling up” the largest element to the last position on the list
- The next pass bubbles up the second largest element, and so on, until after 𝑛−1 passes the list is sorted
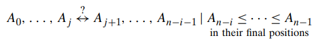


- The number of key comparisons is the same for all arrays of size 𝑛 (almost identical to selection sort)
- However, the number of key swaps depends on the input(In the worst case of decreasing arrays, it is the same as the number of key comparisons)
- We can improve the crude version of bubble sort given above by exploiting the following observation:(if a pass through the list makes no exchanges, the list has been sorted and we can stop the algorithm)
03. Sequential Search
- the algorithm simply compares successive elements of a given list with a given search key until either a match is encountered (successful search) or the list is exhausted without finding a match (unsuccessful search).
- A simple extra trick(if we append the search key to the end of the list, the search for the key will have to be successful, and therefore we can eliminate the end of list check altogether)
- Another straightforward improvement (if a given list is known to be sorted) : searching in such a list can be stopped as soon as an element greater than or equal to the search key is encountered

04. Brute-Force String Matching
The string-matching problem: find a substring of the text that matches the pattern
- pattern: a string of 𝑚 characters to search for
- text: a string of 𝑛 characters to search in
Algorithm
- Step 1 : Align pattern at beginning of text
- Step 2 : Moving from left to right, compare each character of pattern to the corresponding character in text until all characters are found to match (successful search); or a mismatch is detected
- Step 3 : While pattern is not found and the text is not yet exhausted, realign pattern one position to the right and repeat Step 2


- In the worst case, the algorithm makes 𝑚(𝑛−𝑚+1) character comparisons, which puts it in the 𝑂(𝑛𝑚) class
- For a typical word search in a natural language text, however, we should expect that most shifts would happen after very few comparisons
- Therefore, the average-case efficiency should be considerably better than the worst-case efficiency
- For searching in random texts, it has been shown to be linear, i.e., Θ(n)
05. Closest-Pair Problem
Find the two closest points in a set of 𝑛 points
- It is the simplest of a variety of problems in computational geometry that deals with proximity of points in the plane or higher-dimensional spaces
- Points can represent such physical objects as airplanes or post offices as well as database records, statistical samples, DNA sequences, and so on
- Cluster analysis(A bottom-up algorithm begins with each element as a separate cluster and merges them into successively larger clusters by combining the closest pair of clusters)

- Compute the distance between each pair of distinct points
- Find a pair with the smallest distance
06. Convex-Hull Problem
Finding the convex hull for a given set of points in the plane or a higher dimensional space
- one of the most important problems in computational geometry
- convex hulls provide convenient approximations of object shapes and data sets given
- Ex) in computer animation, replacing objects by their convex hulls speeds up collision detection;
- Ex) used for detecting outliers by some statistical techniques
DEFINITION
- A set of points (finite or infinite) in the plane is called convex if for any two points 𝑝 and 𝑞 in the set, the entire line segment with the endpoints at 𝑝 and 𝑞 belongs to the set.
- The convex hull of a set S of points is the smallest convex set containing S.
- An extreme point of a convex set is a point of this set that is not a middle point of any line segment with endpoints in the set.(For example, the extreme points of a triangle are its three vertices, the extreme points of a circle are all the points of its circumference)
How can we solve the convex-hull problem in a brute-force manner?
- A line segment connecting two points 𝒑_𝒊 and 𝒑_𝒋 of a set of 𝑛 points is a part of its convex hull’s boundary if and only if all the other points of the set lie on the same side of the straight line through these two points.
- Repeating this test for every pair of points yields a list of line segments that make up the convex hull’s boundary
- The straight line through two points (x_1, y_1), (x_2, y_2) can be defined by the equation (where 𝑎=𝑦_2−𝑦_1, 𝑏=𝑥_1−𝑥_2, 𝑐=𝑥_1 𝑦_2−𝑦_1 𝑥_2)
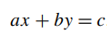
- Such a line divides the plane into two half-planes:(for all the points in one of them, 𝑎𝑥+𝑏𝑦>𝑐, for all the points in the other, 𝑎𝑥+𝑏𝑦<𝑐, for the points on the line itself, of course, 𝑎𝑥+𝑏𝑦=𝑐.)
- Thus, to check whether certain points lie on the same side of the line, we can simply check whether the expression 𝑎𝑥+𝑏𝑦−𝑐 has the same sign for each of these points.
The time efficiency is in 𝑂(𝒏^𝟑)
- for each of 𝑛(𝑛−1)/2 pairs of distinct points,
- we may need to find the sign of 𝑎𝑥+𝑏𝑦−𝑐 for each of the other 𝑛−2 points
07. Exhaustive Search
- Exhaustive search is simply a brute-force approach to combinatorial problems(that ask, explicitly or implicitly, to find a combinatorial object—such as a permutation, a combination, or a subset—that satisfies certain constraints, Many such problems are optimization problems: they ask to find an element that maximizes or minimizes some desired characteristic such as a path length or an assignment cost)
- It suggests generating each and every combinatorial object of the problem, selecting those of them that satisfy all the constraints, and then finding a desired object
- In this chapter, three important problems: (the traveling salesman problem, the knapsack problem, and the assignment problem)
08. Traveling Salesman Problem(TSP)
- to find the shortest tour through a given set of 𝑛 cities that visits each city exactly once before returning to the city where it started
- The problem can be conveniently modeled by a weighted graph, with the graph’s vertices representing the cities and the edge weights specifying the distances
- Alternatively: Find shortest Hamiltonian circuit in a weighted connected graph(A Hamiltonian circuit is defined as a cycle that passes through all the vertices of the graph exactly once, a sequence of 𝑛+1 adjacent vertices 𝑣_𝑖0,𝑣_𝑖1,…,𝑣_𝑖(𝑛−1),𝑣_𝑖0, where the first vertex of the sequence is the same as the last one and all the other 𝑛−1 vertices are distinct)
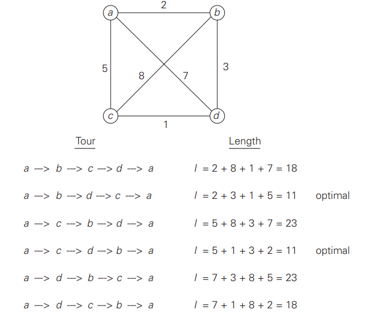
The total number of permutations is 𝟏/𝟐(𝑛−1)!
- Why ½? Three pairs of tours differ only by their direction
- which makes the exhaustive-search approach impractical for all but very small values of 𝑛
09. Knapsack Problem
- Given 𝑛 items of known weights 𝑤_1,𝑤_2,…,𝑤_𝑛and values 𝑣_1,𝑣_2,…,𝑣_𝑛 and a knapsack of capacity 𝑊,
- Find most valuable subset of the items that fit into the knapsack


The exhaustive-search approach to this problem leads to
- generating all the subsets of the set of 𝑛 items given,
- computing the total weight of each subset in order to identify feasible subsets (i.e., the ones with the total weight not exceeding the knapsack capacity),
- and finding a subset of the largest value among them
- the number of subsets of an 𝑛-element set is 2^𝑛 : Ω(2^𝑛) algorithm
10. Assignment Problem
- There are 𝑛 people who need to be assigned to 𝑛 jobs, one person per job
- The cost of assigning person 𝑖 to job 𝑗 is 𝐶[𝑖,𝑗].
- Find an assignment that the minimum total cost.

The problem is
- to select one element in each row of the matrix so that all selected elements are in different columns
- and the total sum of the selected elements is the smallest possible.
- No obvious strategy for finding a solution works here(Selecting the smallest element in each row?)
Solution
- 𝑛-tuples <𝑗_1,…,𝑗_𝑛> in which the 𝑖th component indicates the column of the element selected in the 𝑖th row (i.e., the job number assigned to the 𝑖th person)
- For example, <2, 3, 4, 1> indicates the assignment of Person 1 to Job 2, Person 2 to Job 3, Person 3 to Job 4, and Person 4 to Job 1.
The exhaustive-search approach to the assignment problem
- generating all the permutations of integers 1, 2, . . . , 𝑛,
- computing the total cost of each assignment by summing up the corresponding elements of the cost matrix,
- and finally selecting the one with the smallest sum

11. depth-first search (DFS) and breadth-first search (BFS)
Expand to understand. We will have the opportunity to talk about it in other articles.
'학부공부 > Algorithm_알고리즘' 카테고리의 다른 글
| 06. Greedy Algorithm(2) (0) | 2021.11.18 |
|---|---|
| 05. Greedy Algorithm(1) (0) | 2021.11.18 |
| 03. Brute-force Search(1) (0) | 2021.11.02 |
| 02. 빅오 표기법, 시간복잡도, 공간복잡도(2) (0) | 2021.10.27 |
| 01. 빅오 표기법, 시간복잡도, 공간복잡도(1) (0) | 2021.10.27 |




댓글