효소 작용의 초기속도는 미카엘리스 멘텐 식으로 설명할 수 있다.

이 식과 연관지어 일부사람에게 나타나는 에탄올 민감성을 설명할 수 있다.

일반적으로 사람은 미토콘드리아형과 세포질형의 두 종류의 아세트알데하이드탈수소효소를 가지고 있다. 그러나 에탄올 민감성이 큰 사람은 미토콘드리아형 효소를 구성하는 아미노산이 치환되어 활성이 매우 약한 효소를 가지고 있어 주로 세포질형 효소에 의존하게 된다. 에탄올민감성이 큰 사람이 세포질형 아세트알데하이드탈수소효소에 주로 의존하게 되었을 때 어떤 문제점이 발생할 것으로 예상이 되는가?
14.01. 효소반응 속도론
반응속도론(reaction kinetics)은 화학반응속도와 반응메커니즘에 대해 연구하는 학문분야이다. 반응속도론에서는 반응메커니즘, 반응속도에 영향을 미치는 반응물의 농도, 반응온도, pH 등과 같은 여러 가지 환경인자들에 대한 연구가 주요 대상이다. 이 장은 일반적인 화학반응속도론을 서술하고, 이와 비교하여 효소가 촉매역할을 해서 일어나는 생화학 반응에 대한 속도론은 어떻 게 다른가에 대하여 설명하였다.
14.02. 반응속도의 정의
화학공정이나 생물공정에서 일어나는 반응은 그 속도가 빠른 것도 있고 느린 것도 있다. 반응 속도(chemical reaction rate)는 단위부피당 단위시간에 소모되는 반응물성분 A의 몰농도로 정의되며, SI 단위로 표시하면 mol / m^3․s 가 된다. 반응속도를 반응물 소모를 기준으로 나타 낼 경우 반응이 진행됨에 따라 반응물의 농도가 감소하므로 음의 부호(-)를 붙여야 한다.
예로서 반응물 A가 생성물 R로 변하는 다음과 같은 간단한 반응을 생각해 보자.

이때 반응속도(즉, 반응물의 소실속도)는 다음과 같이 정의된다.

반응속도는 온도, 압력 및 반응계의 조성에 의존되며, 다음과 같이 표현할 수 있다.

여기서 f (C_i)는 각 성분의 농도에 의존되는 함수로서 다음 절의 반응차수에서 논하는 것처럼 반응마다 특정한 형태로 주어진다. k는 반응속도 상수(reaction rate constant)로서 일반 적으로 온도에 의존되며 등온반응(isothermal reaction)인 경우에는 일정한 값을 갖는다.
14.03. 반응차수
반응속도에 영향을 주는 요인은 온도와 반응물의 농도 두 가지인데 이 중에서 농도 의존성을 실험을 통해 구체적으로 결정하여 반응차수를 구한다. 예를 들어, 아래와 같은 비가역반응 (irreversible reaction)의 경우 반응속도식은 다음과 같이 일반식으로 나타낼 수 있다

위 반응속도식에서 α와 β는 반응속도가 반응물 A와 B의 농도에 따라 각각 어떻게 변하는가 를 나타내는 것으로서 반응차수(reaction order)라 한다. 즉, 이때 반응속도는 반응물 A에 대 해서는 α차, 반응물 B에 대해서는 β차이며, 전체적으로는 (α+β)차이다. α와 β는 시간과 농도에 무관한 상수로서 실험적으로 결정해야 하는 값이며, 화학양론계수 a, b와 무관하다.
예를 들어, ascorbic acid가 공기 중의 산소(O2)와 반응하여 dehydroascorbic acid로 변하여 vitamin C로서의 활성을 잃게 되는 경우를 보자.

이때 ascorbic acid의 손실속도식은 실험에 의해 다음과 같이 결정되었다.

여기서 C A는 ascorbic acid의 농도, C O 2는 산소의 농도이다. Ascorbic acid의 분해속도는 ascorbic acid와 산소에 대하여 각각 1차 반응을 나타내고, 전체반응은 2차 반응이다. 반응차수는 실험적으로 결정되는 값으로서 정수가 아닌 경우도 있다. 또한 반응속도식이 간단 한 차수의 형태로 표시할 수 없는 복잡한 반응이 있다. 예를 들어, 효소반응은 다음과 같은 형 태의 Michaelis-Menten 속도식으로 표현되는데, 이 속도식의 반응차수는 고정되어 있는 것이 아니라 기질의 농도(Cs)가 증가함에 따라 1차에서 0차로 변한다.

14.04. 반응속도 상수
반응속도 상수 k는 온도에 따라 변할 뿐 아니라 반응에 사용하는 용매, 촉매농도, pH 등 환경 조건에 따라서 변한다. 그러나 일반적으로 다른 환경조건은 일정하다고 생각하고 k를 온도만 의 함수로 나타내는 경우가 많다. 반응속도 상수 k는 반응물이나 생성물의 농도에 무관하므로 특정 온도에서 반응속도의 크기를 나타내는 데 매우 유용하게 사용된다. 속도상수의 단위는 총 괄 반응차수에 의존한다. 예를 들어, 1차 반응의 경우 속도상수의 단위는 시간의 역수(sec^-1)이 다.
14.05. Reaction rate expression for a simple constant volume reaction system
반응속도식은 여러 가지 수학적 형태로 표현되며, 반응차수도 항상 정수는 아니다. 그러나 화학 공정이나 생물공정에서 많은 반응은 단순한 형태로 근사적으로 표현될 수 있으며 반응차수도 0 차 또는 1차인 경우가 많다.
14.06. Irreversible first order reaction kinetics
1차 반응은 반응속도가 한 종류의 반응물질의 농도에 비례한다. 비가역(irreversible)이란 반응 물이 생성물로 전환될 뿐이며 생성물이 다시 반응물로 복귀되는 일이 없음을 말한다. 다음과 같은 비가역적인 단분자반응(unimolecular reaction)을 고려해 보자.

이 반응이 1차 반응(first order reaction)을 따른다면 그 속도식은

으로 나타낼 수 있다. 우측 두 항을 변수 분리하여 적분하면 다음과 같이 표시된다.

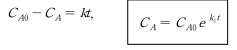
위 식을 임의의 시간 t 에 반응물 A의 농도 CA를 구하는 식으로 표현하면

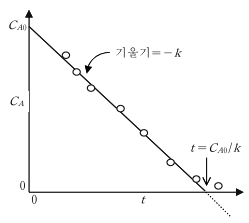
로 나타낼 수 있다. 즉, A의 농도는 반응이 진행됨에 따라 대수 함수적으로 감소한다. 아래그림은 비가역 1차 반응의 경우 반응물 농도의 대수값과 반 응시간 사이에 직선관계가 있음을 나타내고 있다. 실험에 의해 얻어진 반응시 간에 따른 농도(C_A) 데이터로부터 구한 - ln (C_A /C_A0 )값을 반응시간 t 에 대해 구하고, 동그라미(open circle)로 표시된 데이터를 통과하며 원점을 지나는 직선식을 최소자승법(least square method)에 의해 구한다. 이 직선의 기울기가 반응속도 상수 k 값이다.

1차 반응속도는 초기농도(C_A0)에 무관하다. 1차 반응의 경우 반응속도를 반감기(half life)로 나타내면 편리할 때가 많다. 반감기는 반응물질의 농도(C_A)가 초기농도(C_A0)의 절반으로 감소하는데 걸리는 시간을 의미하며 t_(1/2) 로 표시한다. C _A = 1/2 (C_A0)를 대입하면 1차 반응의 반감기는 농도에 무관하 고 반응속도 상수에 반비례함을 알 수 있다.
14.07. Zero order reaction kinetics
반응속도가 반응물의 농도에 전혀 영향을 받지 않는 반응을 0차 반응이라 한다. 0차 반응속도 식은 다음과 같이 표시할 수 있다.

위 식의 우측의 두 항을 적분하면
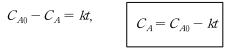
반응물의 소모된 양, 즉 (C_A0-C_A)가 반응시간에 비례함을 의미한다. 0차 반응인 경우에는 농도-시간 실험데이터로부터 각 반응시간에서의 잔존 반응물의농도 C_A를 시간 t 에 대해 그래프를 그리면 직선을 얻게 되며, 이 직선의 기울기 값으로부터 반응 속도 상수 k를 구할 수 있다. 일반적으로 화학반응은 초기에 반응물질의 농도(C_A0)가 충분히 높을 때에는 0차 반응을 나타내다가 농도가 어느 수준 이하로 감소하면 반응성이 농도에 의존하게 되어 반응차수가 증가하게 된다.
14.08. Irreversible serial reaction
효소에 의한 생화학 반응은 대개 여러 단계의 연속된 반응이다. 가장 간단한 경우로서 2단계 비가역 연속반응에서 반응물, 중간생성물, 최종생성물의 농도가 시간에 따라 어떻게 변화하는 지 알아보자. 다음과 같은 연속 단분자형 1차 반응에서 세 가지 성분에 대한 속도식은 아래와 같이 표현된다.
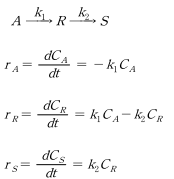
위 세 개의 선형 1차 미분방정식을 연립하여 풀면 반응물(A), 중간생성물(R) 및 최종생성물(S) 의 농도가 시간의 함수로 구해진다. 초기에 R이나 S는 존재 하지 않고, A의 농도는 C_A0에서 반응을 개시하여 세 성분들의 농도변화가 시간에 따라 어떻게 되는지 알아보자. 2번째 식을 적분하면 아래와 같이 된다.
또는 시간에 따른 농도변화를 구하기 위해 위 식에 3번째 식을 대입하면 미분방정식을 얻는다.
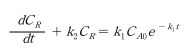
이는 1차 선형 미분방정식 형태이다.
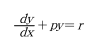
해를 구하면,
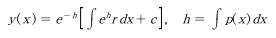

t = 0일 때 C_R = 0이므로
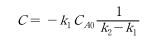
대입하면

전체 몰수 변화는 없으므로 양론으로부터 반응물, 중간생성물, 최종생성물 사이에는 다음 관계가 성립된다.
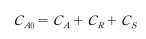
대입하면 최종생성물 S의 시간에 따른 농도변화를 구할 수 있다.
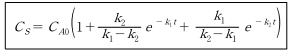
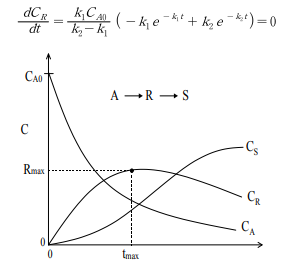
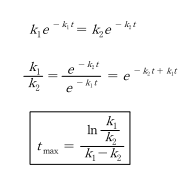
반응물질(A)은 지속적으로 감소하며, 최종생성물(S)은 S형으로 증가한다. 중간생성물(R)은 최대값을 갖는다. R의 최대농도 와 그때의 시간은 k_1과 k_2에 의해 정해진다. 미분하여 dC_R/dt = 0 일 때 다음과 같이 시간(t)을 구한다.
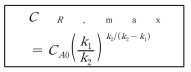
14.09. 반응차수가 변동되는 반응속도식
속도식의 탐색에서 고농도에서는 데이터가 어떤 반응차수에 잘 부합되는 데 저온도에서는 다른 반응차수에 부합되는 것을 볼 수 있다. 반응물의 농도감소에 따라 낮은 차수에서 높은 차수로 이동하는 반응을 아래와 같이 표시하면

이것의 반응속도는 다음과 같이 표현될 수 있다.
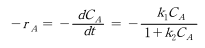
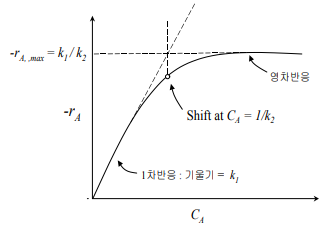
이 속도식으로부터 고농도의 C_A(또는 k_2C_A≫1)에서 이 반응은 속도상수가 k_1/k_2인 0차 반응이다. 그러나 저농도의 C_A(또는 k_2C_A≪1)에서 이 반응은 속도상수가 k_1인 1차 반응으로 바뀐다. 이러한 형태의 반응속도식을 일반적으로 Langmuir- Hinshelwood 속도식이라고 부르며, 이 식은 생물공학에서 효소 촉매반응의 반응식인 MichaelisMenten 식과 유사한 식이다.
14.10. Enzyme reaction kinetics
단일 기질-효소 촉매반응의 속도식은 Michaelis-Menten 속도식을 기본으로 한다. 효소속도론 의 정성적인 특징은 Langmuir-Hinshelwood 속도론과 비슷하다. 생물계에서는 다기질-다효 소반응과 같은 보다 복잡한 효소-기질간 상호작용이 일어날 수 있다. 효소는 기질과 결합할 수 있는 활성부위의 숫자가 일정하기 때문에 높은 기질농도에서는 활성부위 모두가 기질과 결합하 여 효소가 포화되는 상태가 된다. 효소 반응속도론은 다음과 같이 효소(E) - 기질(S)의 복합체[ES] 형성단계의 가역반응과 ES 복합체의 비가역 해리단계의 2단계의 반응체계로부터 구할 수 있다.
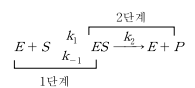
위 반응체계는 ES 복합체가 다소 빠른 속도로 형성되고 두번째 단계의 역반응속도를 무시한다는 가정을 전제로 한다. 두번째 반응의 비가역가정은 반응초기에 생성물의 축적을 무시할 때 성립된다. 위의 2단계 반응체계로부터 효소 반응속도식(즉, Michaelis-Menten kinetics)을 유도하기 위해서 다음의 두 가지 가정 중에 한 가지를 사용한다.

- 빠른 평형(rapid equilibrium approach)
- 가정 유사 정상상태(quasi-steady-state approach) 가정
14.11. 단순 효소속도론의 수학적 모형 (Michealis-Menten Kinetics)
유사 정상상태 또는 빠른 평형을 가정하여 효소 반응속도식을 유도할 때 초기 단계는 두 경우 가 동일하다. 반응속도 v 는 생성물의 생성속도 또는 기질의 소모 속도로서 moles/L․s의 단위를 갖는다.
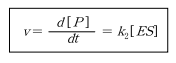
여기서 ES 복합체의 시간에 따른 변화속도는 식 (8.34)와 같다. 이 식은 식 (8.32)의 1단계에서 E와 S의 반응에 의한 ES 복합체의 생성, ES의 분해에 의한 E와 S로의 역반응 및 2단계에서 ES의 분해에 의한 E와 P 의 생성속도를 고려한 것이다.
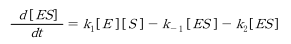
효소에 대한 보존식은 다음과 같다.

복합체 [ES]의 농도를 측정하는 것은 어려우므로 빠른 평형이나 유사 정상상태 를 가정하여 [ES]를 대신할 표현식을 찾는다.
빠른 평형을 가정한 Michaelis-Menten 속도식 유도
빠른 평형가정은 효소와 기질이 반응하여 ES 복합체를 형성하는 과정이 빠르게 도달한다고 가 정한 것이다. 정반응속도와 역반응속도가 동일하다고 하면
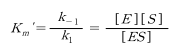
효소가 보존된다면 [E] = [E_0] - [ES]이므로
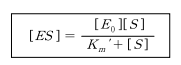
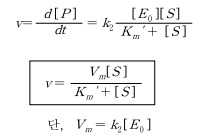
Km' 은 최대 반응속도의 1/2의 속도에 해당하는 기질의 농도로서 기질과 효소의 친화도를 나타 내고, Km'이 작다는 것은 효소의 기질에 대한 친화도가 높다는 것을 나타낸다.
유사 정상상태를 가정한 Michaelis-Menten 속도식 유도
대부분의 실험은 초기에는 효소농도에 비해 충분히 높은 기질농도를 유지하는 회분식 반응을 이용한다. 이 경우 효소의 농도([E_0])가 충분히 낮기 때문에 d [ES ] / dt ≈ 0 이라 가정할 수 있 고 이를 유사 정상상태라고 한다.
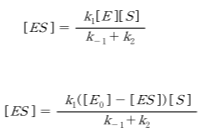
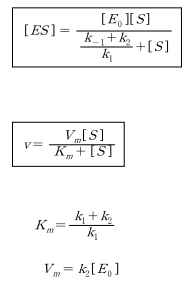
위에서 보듯이 두 가지 가정 중에서 어느 것을 사용하던지 동일한 결과가 유도되는 것을 알 수 있다.
14.12. Km값의 응용
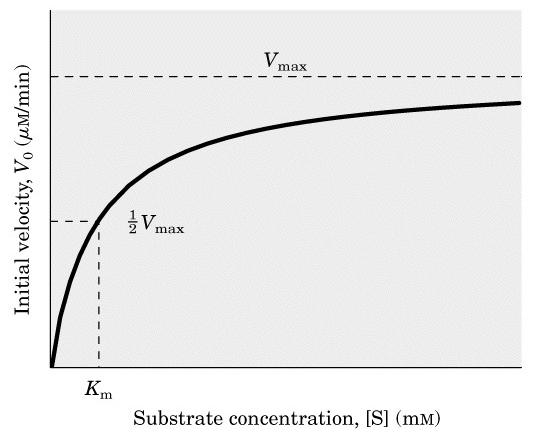
미카엘리스 상수 Km은 효소반응에서 특정 기질에 대한 속도 상수이다. 대부분의 경우에서 미카엘리스 상수는 대응하는 기질에 대한 효소의 친화성을 나타낸다. 즉, Km을 이해하면 특정 효소에 어떤 기질이 친화도를 갖는지 파악할 수 있는 것이다. 식에서 [S]자리에 Km을 대입하면 V_0=1/2Vmax가 나온다. 즉, Km은 반응속도가 최대값의 절반일때의 기질 농도를 의미하고 기질 농도가 Km 정도 있을 때 몸에서 유의미한 반응이 일어난다.
k_1의 속도가 k_2보다 훨씬 빠르다고 가정하면 ES는 생성물을 만드는 것보다 해리되는 속도가 훨씬 빠를 것이다. Km = (k-1 + k2)/k1 값의 정의에서 k2가 너무 작아 Km = k-1/k1으로 표시할 수 있다.
Km = k-1/k1 = [E]*[S] / [ES] = Kes로 [ES]가 해리되는 값과 같다. 여기서 k1이 분모이기 때문에 [ES]가 반응물로 작용한 것이다.
Km = Kes
따라서 Km 값이 크면 ES 복합체의 결합이 약하고 Km 값이 작으면 ES 복합체의 결합이 강하다고 생각할 수 있다.
알로스테릭 효소 (allosteric enzyme) 속도론, 저해반응에서의 효소 속도론, 기질 저해 작용이 있을 때의 효소 속도식, 반응속도의 온도 의존성, 효소 반응속도의 pH 의존성등에 관한 추가적인 설명은 아래의 PDF로 대체한다.
Solution
세포질형 아세트알데하이드탈수소효소는 Km이 커서 에탄올의 분해산물인 아세트알데하이드의 분해가 매우 느리고 혈액으로 많이 빠져나와 생리적인 영향을 준다. 아세트알데하이드에 의해 얼굴이 붉어지고 심장이 빨리 뛰게 된다.
'Science > Life science_생명과학' 카테고리의 다른 글
| 생명과학 16. 어류 아가미 (0) | 2021.10.26 |
|---|---|
| 생명과학15. 심장병 환자 (0) | 2021.10.26 |
| 생명과학13. 글루타민 합성 (0) | 2021.10.25 |
| 생명과학12. 탄소고정 (0) | 2021.10.25 |
| 생명과학11. 수소이온 (0) | 2021.10.25 |


댓글