1.1. Problem
- Three missionaries and three cannibals must cross a river.
- They cross the river using a boat which can carry at most two people.
- On each side of the river, cannibals must not outnumber missionaries, otherwise cannibals will eat missionaries.
| Order | Left | Boat | Right |
| 0 | MMM CCC | ||
| 1 | MMMC | CC -> | CC |
| 2 | MMMCC | <- C | C |
| 3 | MMM | CC -> | CCC |
| 4 | MMMC | <- C | CC |
| 5 | MC | MM -> | MM CC |
| 6 | MMCC | <- MC | M C |
| 7 | CC | MM -> | MMM C |
| 8 | CCC | <- C | MMM |
| 9 | C | CC -> | MMM CC |
| 10 | CC | <- C | MMM C |
| 11 | CC -> | MMM CCC |
Implement combinational logic of the problem
① Input : Present state of missionaries and cannibals, Direction (Left or Right)
② Output : Next state of missionaries and cannibals
③ If the present state is the last state (everyone crossed the river), the next state is the initial state (everyone is on the start point)
④ If the present state is far from the solution, the next state is the initial state (everyone is on the start point)
⑤ Must implement with gate-level
Module : missionary_cannibal
- Input1 : 2bit (input [1:0] missionary_curr)
- Input2 : 2bit (input [1:0] cannibal_curr)
- Input3 : 1bit (input direction) – Left 0, Right 1
- Output1: 2bit (output [1:0] missionary_next)
- Output2: 2bit (output [1:0] cannibal_next)
1.2. Project summary

Practice truth table on description of the situation. (By, PPT 4page)
The above situation is perhaps the best way to solve the problem. We can write the whole truth table based on TABLE 1. The new truth table is prepared as close to TABLE 1 as possible. However, when writing a truth table, we should be careful about the second limiting condition of the problem and the direction away from solving the problem.
After writing the truth table, set up a Boolean function expression for the output based on the truth table. Where Boolean function expressions are written for implementation in the gate level as much as possible.(By, PPT 5page Project Specification – clause 5)
When the boolean function expression is completed, make a module(Verilog code) in ModelSim and test it using the appropriate input script. A suitable input script will be provided by the truth table. What is important is to implement a combinational logic circuit with five inputs and four outputs.
1.3. Module decription (Include description of implement)
1.3.1. Truth table

Shaded parts of the truth table will be described in more detail on the next page.
missionary_curr : a variable that stores the number of missionary at the starting point in binary.
cannibal_curr : a variable that stores the number of cannibal at the starting point in binary.
direction : Left is 0 and right is 1
missionary_next : a variable that stores the number of missionary at the destination in binary.
cannibal_next : a variable that stores the number of cannibal at the destination in binary.
1.3.2. Input and output
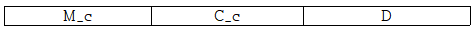
The program receives the current status of missionaries and cannibals and direction as input.
M_c : Missionaries_current state, C_c : Cannibals_current state, D : Direction

The program outputs the following states of the missionaries and cannibals.
M_n : Missionaries_next state, C_c : Cannibals_next state
1.3.3. Explanation of special cases

This situation is that the current situation is far from the solution and either reset the state or it has already been resolved and reset the state. (By, PPT 5page Project Specification – clause 3, 4)

This situation is that everyone has moved to the other side of the river. If this situation enters the input, the value will be initialized by line 1 and line 2 of the truth table.
1.3.4. Boolean function expression
M_c, M_n, C_c and C_n are 2-bit bundles, but for convenience, they are spelled M_c1, M_c2.
(That is, M_c is
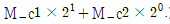
)
It is marked A,B,C,D,E again in order.

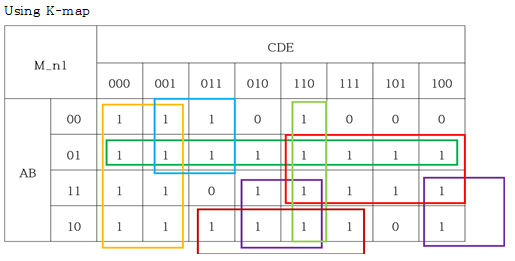
= A'B + AE' + BC + C'D' + A'C'E + CDE' + AB'D
In addition to the K-MAP method, this can be simplified in the same way in accordance with several rules on boolean function about simplification.

= C'D' + C'E + CDE' + AE' + AD + BC

= A'B + AB' + C'D'E + DE' + CE' + A'C'
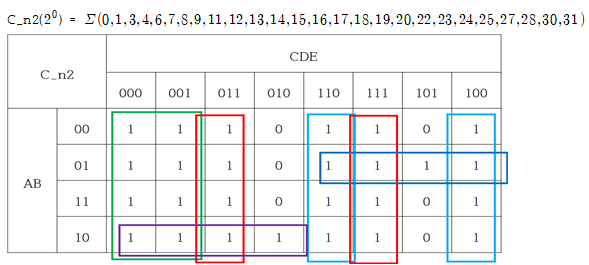
= C'D' + CE' + DE + A'BE + AB'C
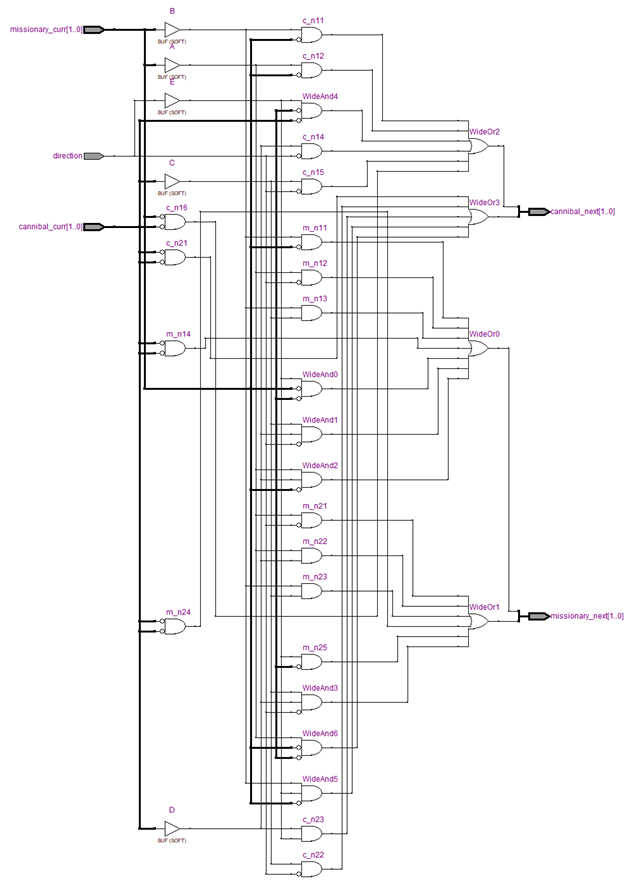
1.4. HDL code (Include program comment)
CODE
//COSE221 : Term project : Missionaries and cannibals problem
//Module declaration at the beginning
//module name and pin declaration outside module
module missionary_cannibal
(
missionary_curr,
cannibal_curr,
direction,
missionary_next,
cannibal_next
);
//input
//[1:0] a two-bit bus
input [1:0] missionary_curr;
input [1:0] cannibal_curr;
input direction;
//ouput
output [1:0] missionary_next;
output [1:0] cannibal_next;
//wire : Mediation unit for connection to another gate (simple physical connection line)
//These declarations help readability. A is more intuitive and convenient than Missionary_curr[0].
wire nA, nB, nC, nD, nE, A, B, C, D, E;
buf (A, missionary_curr[1]);
buf (B, missionary_curr[0]);
buf (C, cannibal_curr[1]);
buf (D, cannibal_curr[0]);
buf (E, direction);
not (nA, missionary_curr[1]);
not (nB, missionary_curr[0]);
not (nC, cannibal_curr[1]);
not (nD, cannibal_curr[0]);
not (nE, direction);
//missionary_next[1]
wire m_n11, m_n12, m_n13, m_n14, m_n15, m_n16, m_n17;
and (m_n11, nA, B); //A'B
and (m_n12, A, nE); //AE'
and (m_n13, B, C); //BC
and (m_n14, nC, nD); //C'D'
and (m_n15, nA, nC, E); //A'C'E
and (m_n16, C, D, nE); //CDE'
and (m_n17, A, nB, D); //AB'D
//A'B + AE' + BC + C'D' + A'C'E + CDE' + AB'D
or (missionary_next[1], m_n11, m_n12, m_n13, m_n14, m_n15, m_n16, m_n17);
//missionary_next[0]
wire m_n21, m_n22, m_n23, m_n24, m_n25, m_n26;
and (m_n21, A, nE); //AE'
and (m_n22, A, D); //AD
and (m_n23, B, C); //BC
and (m_n24, nC, nD); //C'D'
and (m_n25, nC, E); //C'E
and (m_n26, C, D, nE); //CDE'
//C'D' + C'E + CDE' + AE' + AD + BC
or (missionary_next[0], m_n21, m_n22, m_n23, m_n24, m_n25, m_n26);
//cannibal_next[1]
wire c_n11, c_n12, c_n13, c_n14, c_n15, c_n16;
and (c_n11, nA, B); //A'B
and (c_n12, A, nB); //AB'
and (c_n13, nC, nD, E); //C'D'E
and (c_n14, D, nE); //DE'
and (c_n15, C, nE); //CE'
and (c_n16, nA, nC); //A'C'
//A'B + AB' + C'D'E + DE' + CE' + A'C'
or(cannibal_next[1], c_n11, c_n12, c_n13, c_n14, c_n15, c_n16);
//cannibal_next[0]
wire c_n21, c_n22, c_n23, c_n24, c_n25;
and (c_n21, nC, nD); //C'D'
and (c_n22, C, nE); //CE'
and (c_n23, D, E); //DE
and (c_n24, nA, B, E); //A'BE
and (c_n25, A, nB, nC); //AB'C'
//C'D' + CE' + DE + A'BE + AB'C'
or(cannibal_next[0], c_n21, c_n22, c_n23, c_n24, c_n25);
//module end declaration
endmodule
1.5. Simulation screenshot


Logic design & Computer Architecture 카테고리의 출처는 2020년도 1학기 COSE221 논리설계 과목의 정성우 교수님 수업과 2020년도 2학기 COSE222 컴퓨터구조 과목의 정성우 교수님 수업입니다.
'학부공부 > Logic Design & Computer Architecture' 카테고리의 다른 글
| 8. ARM 5stage pipeline report 2 [Computer Architecture] (0) | 2021.12.02 |
|---|---|
| 7. ARM 5stage pipeline report 1 [Computer Architecture] (4) | 2021.12.02 |
| 6. ARM instruction 분석 report [Computer Architecture] (0) | 2021.12.02 |
| 3. Project 3_Calculator [Logic Design] (0) | 2021.12.02 |
| 2. Project 2_Missionaries and cannibals problem [Logic Design] (0) | 2021.12.02 |




댓글